Pytorch 安装

线性模型

1. DataSet :smile:
2. Model
3. Training
4. Inferring

• 过拟合：学习的时候 把噪声也学习进来了。

• 泛化能力：可以正确识别在测试集中没有的数据。

通常是得不到测试集的结果，所以为了防止深度学习过程中的过拟合以及增加模型的泛化能力，需要再次将训练集分为训练集和开发集，但训练集训练完成后，需要放到开发集中进行测试，如果满足要求，再把开发集合并到训练集中，再进行训练。

• 损失模型（loss）:在机器学习中评估的方式

• 平均平方误差（MSE）：

\[ cost=\frac{1}{N}\sum_{n=1}^{N}{(\hat{y}_n-y_n)^2} \]

梯度下降法

梯度下降法（Gradient Descent）:

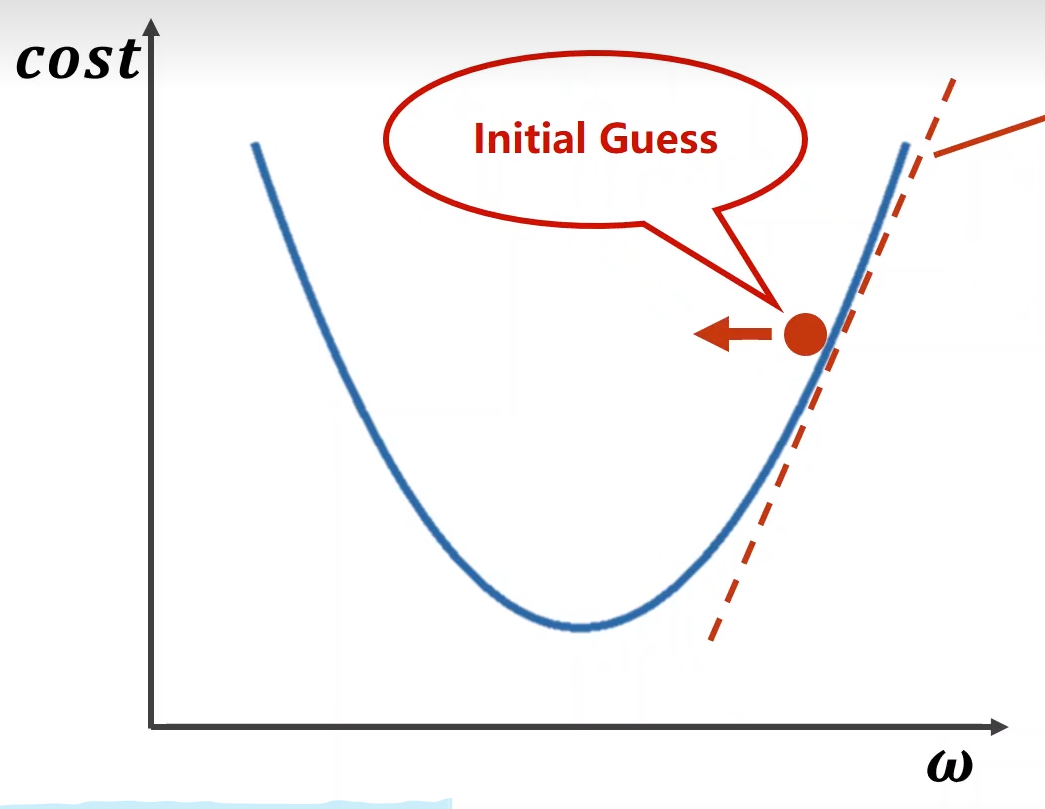
\[ Gradient = \frac{\partial{cost}}{\partial{w}} \] 倒数的负方向就是\(cost\)减小的方向：

核心算法： \[ \omega=\omega-\alpha\frac{\partial{cost}}{\partial{w}} \]

• \(\alpha\)为学习率

梯度下降法体现了贪心的思想，只找当前最好的选择，如果遇到非凸函数，只能找到局部最优解。

需要说明的是，在神经网络中很难陷入到局部最优点，但是遇到鞍点后，梯度计算结果为0，会导致\(\omega\)无法增加。

如果发现\(cost\)发散，证明训练失败，最有可能的原因是因为学习率\(\alpha\)太大。

随机梯度下降法： \[ Gradient = \frac{\partial{loss}}{\partial{w}} \] \(cost\)为所有样本的损失函数，当遇到鞍点时可能会陷住无法推进，将所有样本的损失换成单个样本的损失，利用单个样本的随机噪声可能会推动继续前进。

如果利用随机梯度下降法，下一个样本\(\omega\)的计算是需要上一个样本的\(\omega\)值，就不能并行计算，而梯度下降法则可以实现并行计算。

批量随机梯度下降法

作为梯度下降法和随机梯度下降法的折中办法，批量随机梯度下降法将多个样本进行分组，在每个组内进行随机梯度下架法。

反向传播

张量 Tensor

Tensor是PyTorch里面最基本的数据类型，可以是标量，向量，矩阵，甚至是高维的Tensor，与Numpy中的多维数组非常类似。Tensor还提供了GPU计算和自动求梯度等很多功能，使得Tensor更加适合深度学习。

Tensor是一个类，里面有两个非常重要的成员，data和grad：

• data中存放的是权重\(\omega\)​
• grad中存放的是损失函数对于\(\omega\)的导数：\(\displaystyle{\frac{\partial{loss}}{\partial{\omega}}}\)

分类问题

输出值应该为概率，计算输入值属于输出值每一个分类的概率，所有分类的概率值相加应该等于1，然后将概率值进行排序，去概率最大的那个为最终结果。

与分类任务不同的是，回归任务是预测一个或者多个连续变量，回归任务的核心是通过学习输入变量和输出变量之间的关系来预测未来的输出值。

回归任务的特点是：

1. 目标变量是连续的，回归任务的输出变量可以取任意实数值。
2. 回归任务存在损失函数，用来衡量预测值与实际值之间的差距。

Sigmoid 函数

通过sigmoid函数可以将输出值对应到0~1的范围内。 \[ y=\frac{1}{1+e^{-x}} \] 在论文中Sigmoid函数一般简写为\(\sigma(x)\)

交叉熵

\[ loss=-(y\log \hat{y}+(1-y)log(1-\hat{y})) \]

加载数据集

• Epoch：所有样本参与一次训练指的是Epoch

• Batch-Size：一次训练时所用的样本数量

• Iteration：所有样本所分成的份数，即所有样本数除以Batch-Size数