控制:三个坐标系与运动学方程
Apollo 控制算法
采用 PID + LQR 算法,大多数选择MPC, 但是MPC的计算量太大
默认已经有一条路径规划
控制
- 油门/刹车:arrow_right:力:arrow_right:加速度:arrow_right:速度:arrow_right:位置
- 方向盘:arrow_right:前轮转角:arrow_right:横向位移and航向角
三个坐标系
- 绝对坐标系,大地坐标系(X-Y)
- 车身坐标系(x-y)
- 自然坐标系(Frenet坐标系)
现在一律采用右手系,符合右手拇指指向 X 轴,食指指向 Y 轴,中指指向 Z 轴,算是符合右手系。反之是左手系,一般数学物理类是右手系,计算机或者视觉专业是左手系。
一般对车进行建模分析的时候都看成自行车模型,把四个轮子变成两个轮子,认为车是完全的左右对称的,并且左右轮距相对于轨迹来说可以忽略不计。进行简化
速度计算
用理论力学的顺心法
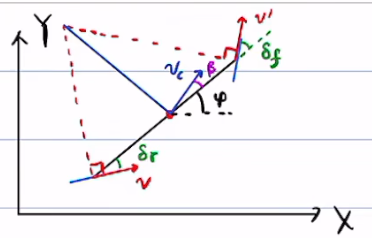
垂线的方向就是质心速度的方向,车的质心速度方向一般和车的轴线方向一般不会重合,车的轴线方向和大地坐标系的 X 方向一般也不是重合的。所以要定义两个角度
\(\phi\) 横摆角:车的轴线与\(\overrightarrow{X}\)方向的夹角,绝对坐标系下
\(\beta\)质心侧偏角:质心速度与\(\overrightarrow{x}\)方向的夹角,车身坐标系下
\(\phi+\beta\)航向角:质心速度与\(\overrightarrow{X}\)方向的夹角,绝对坐标系下
\(\delta_{f}\):"前轮转角",\(\delta_{r}\):"后轮转角",因为轮胎不是纯钢体,所以会有侧偏。车身坐标系下
三个假设:左右对称,轮距可以忽略不计,车的轮子是个刚性的轮子
模型建立
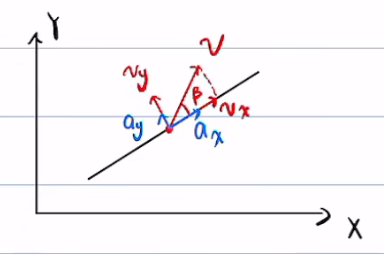
\(v_{x}\):纵向车速,\(a_x\):纵向加速度。
\(v_y\):侧向车速,\(a_y\):侧向加速度。
建立微分方程组:
几何关系:运动学模型
牛顿力学:动力学模型
运动学模型
\[\dot{X}=v\cos(\beta+\phi)\]
\[\dot{Y}=v\sin(\beta+\phi)\]
\[\dot{\phi}=\dfrac{v}{R}\]
上述式子体现了速度\(v\)对\(\dot{X},\dot{Y},\dot{\phi}\) 影响,下面推导横摆角对其的影响
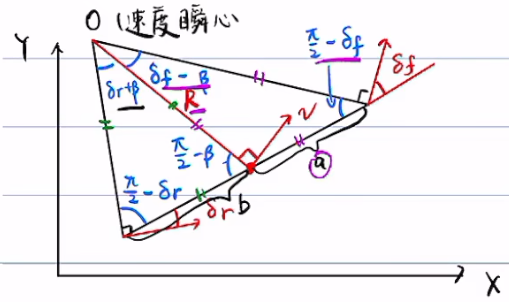
正弦定理:
设质心到前轮的距离为\(a\),到后轮的距离为\(b\)
\(\dfrac{a}{\sin(\delta_f-\beta)}=\dfrac{R}{\sin(\frac{\pi}{2}-\delta_f)}\)
\(\dfrac{b}{\sin(\delta_r+\beta)}=\dfrac{R}{\sin(\dfrac{\pi}{2}-\delta_r)}\)
\(\dfrac{a}{R}=\dfrac{\sin(\delta_f-\beta)}{\sin(\frac{\pi}{2}-\delta_f)}=\dfrac{\sin\delta_f\cos\beta-\sin\beta\cos\delta_f}{\cos\delta_f}=\tan\delta_f\cos\beta-\sin\beta\)
\(\dfrac{b}{R}=\dfrac{\sin(\delta_r+\beta)}{\sin(\dfrac{\pi}{2}-\delta_r)}=\dfrac{\sin\delta_r\cos\beta+\sin\beta\cos\delta_r}{\cos\delta_r}=\tan\delta_r\cos\beta+\sin\beta\)
因为质心会随着载重变化,所以选择一种不变的量表示比较好
\(\dfrac{a+b}{R}=(\tan\delta_f\cos\beta+\tan\delta_r\cos\beta)\) :arrow_right: \(\dfrac{1}{R}=\dfrac{\tan\delta_f\cos\beta+\tan\delta_r\cos\beta}{L}\) 其中 \(L=a+b\) 为车的轴距
因此:运动学方程为
\[\dot{X}=v\cos(\beta+\phi)\]
\[\dot{Y}=v\sin(\beta+\phi)\]
\[\dot{\phi}=\dfrac{v}{R}=\dfrac{v(\tan\delta_f\cos\beta+\tan\delta_r\cos\beta)}{L}\]
在低速情况下,认为车不会发生侧向滑动(漂移)即\(v_{y}\approx0\),因此,根据模型建立的第一个图,\(\beta=\arctan\dfrac{v_y}{y_x}\approx0\)
一般后轮不会转向,所以在低速情况下,\(\delta_r\approx0\)
因此可以将运动学方程近似为
\[\dot{X}=v\cos\phi\]
\[\dot{Y}=v\sin\phi\]
\[\dot{\phi}=\dfrac{v}{R}=\dfrac{v\tan\delta_f}{L}\]
又因为\(\beta\approx0\),所以 横摆角\(\approx\)航向角
其中\(\phi\) 为横摆角,\(v\)为质心速度