决策规划:参考线模块
决策规划总体概览(已有导航路径,决策规划流程)
- 定位+导航:生成参考线
- 静态障碍物投影到以参考线为坐标轴的frenet坐标轴上
- 决策算法对障碍物做决策(往左绕,往右绕,忽略),开辟最优凸空间
- 规划算法在凸空间中搜索出最优的路径
- 后处理,在规划轨迹中选取一个点,坐标转换成Cartesian,输出给控制去跟踪
参考线
参考线是解决方案,解决导航路径过长,不平滑的问题
- 过长的路径不利于坐标转换
- 过长的路径,障碍物投影可能不唯一
- 不平滑
解决方案:截取一小段轨迹做平滑,将平滑后的轨迹作为参考线
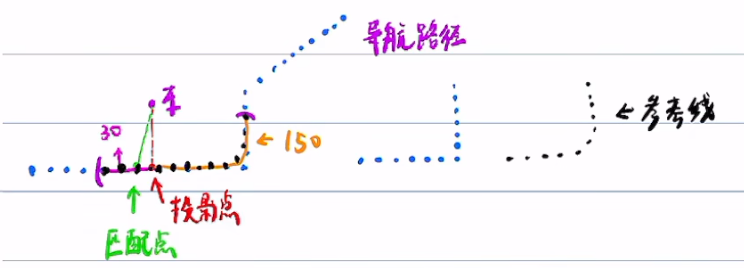
每个规划周期内,找到车在导航路径中的投影点,以投影点为坐标原点,往后取30米,往前取150米范围内的点,做平滑,平滑后的点的集合成为参考线。
参考线平滑算法
平滑性因素

\(|\overrightarrow{P_{1}P_{3}}|\):衡量平滑与不平滑的标准,\(|\overrightarrow{P_{1}P_{3}}|\)越小越平滑。缺点:虽然平滑了,但是几何形状差距大。
道路几何因素
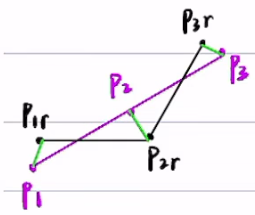
\(|\overrightarrow{P_{1}P_{1r}}|+|\overrightarrow{P_{2}P_{2r}}|+|\overrightarrow{P_{3}P_{3r}}|\)越小,越接近原几何路径。
长度要尽可能均匀和紧凑
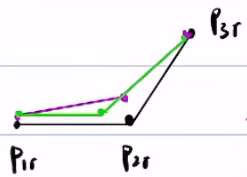
\(|\overrightarrow{P_{1}P_{2}}|^2+|\overrightarrow{P_{1}P_{3}}|^2\)越小,越均匀,紧凑。
代价函数

已知:\(x_{1r}...x_{3r},y_{1r}...y_{3r}\)
未知:\(x_{1}...x_{3},y_{1}...y_{3}\)
代价函数:
\[cost function = \\ w_{1}\{\sum_{i=1}^3(x_i-x_{ir})^2+(y_i-y_{ir})^2\}+\\w_2\{(x_1+x_3-2x_2)^2+(y_1+y_3-2y_2)^2\}+\\w_3\{\sum_{i=1}^2(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2\}\]
①与原路径点相似的代价,②平滑代价,③紧凑代价
平滑代价:
\(W_{cost\_smooth}\cdot x^TA^T_1A_1x\ ,A_1size=(2n,2n-4)\)
紧凑代价:
\(W_{cost\_length}\cdot x^TA^T_2A_2x\ ,A_2size=(2n,2n-2)\)
几何相似代价:
\(W_{cost\_ref}\cdot x^TA_3^TA_3x+f^Tx\)
\(\sum_{i=1}^n(x_{ir}-y_{ir})^2\)是个常数,可以忽略。
二次规划问题
二次规划问题的目标函数是变量的二次函数,而约束条件可以是线性的,一般形式如下:
\[Minimize: \dfrac{1}{2}x^TQx+c^Tx\]
\[Subject\ to: Ax\leq b ,Ex = d\]
其中:
- \(x\)是一个\(n\)维向量,表示决策变量
- \(Q\)是一个\(n\times n\)的对称矩阵,表示目标函数中变量的二次项系数
- \(c\)是一个\(n\)维向量,表示目标函数中变量的一次项系数
- \(A\)是一个\(m\times n\)的矩阵,\(b\)是一个\(m\)维向量,定义了\(m\)个线性不等式约束
- \(E\)是一个\(p\times n\)的矩阵,\(d\)是一个\(p\)维向量,定义了\(p\)个线性等式约束
针对参考线
二次规划:
\(=\dfrac{1}{2}x^THx+f^Tx\)
\(= x^T\dfrac{H}{2}x+f^Tx\)
此处:\(H=2(W_{smooth}A^T_1A_1+W_{length}A^T_2A_2+W_{ref}A^T_3A_3)\)
约束:
\(x\)与\(x_{ref}\)不要离太远,\(|x-x_{ref}|\leq buff\)
曲率约束:
曲率约束是一种非线性约束,一般与车的最大侧向加速度有关(有些弯过不去),放到后面考虑。
Fem smoother平滑算法
优点:优化变量较少
缺点:无法保证曲率是连续的,添加曲率约束求解比较麻烦
参考线是决策规划的基础和前提,必须要快,采用方案如下:
- 减少规划频率,规划算法每100ms执行一次,控制算法每10ms执行一次
- 充分利用上个周期计算的结果
找匹配点
普通算法:每一个规划周期计算一遍,太慢,导航路径很可能很长,遍历费时
改进算法:
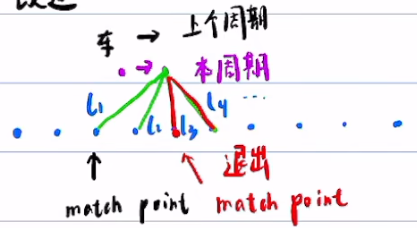
以上个周期的 match point 为起点做遍历,一旦有\(l_{i+1}>l_i\),立刻退出遍历,\(l_i\)对应的点作为本周期的匹配点
找匹配点的方向:
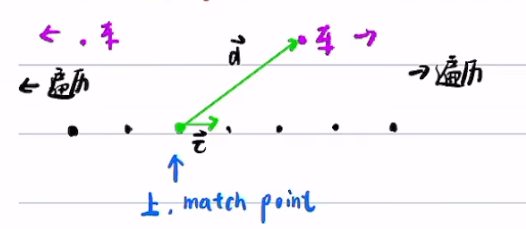
如果车往前,就往前遍历,如果车往后,就往后遍历:
\(\overrightarrow{d} \cdot \overrightarrow{\tau}>0\):向前遍历
\(\overrightarrow{d} \cdot \overrightarrow{\tau}<0\):向后遍历
\(|\overrightarrow{d} \cdot \overrightarrow{\tau}|<10^{-3}\):本周期的match point 等于上个周期的match point
本质有点像梯度下降
此方法可以大大加速找匹配点的算法,但只适用于在上个匹配点结果附近只有一个极小值点。
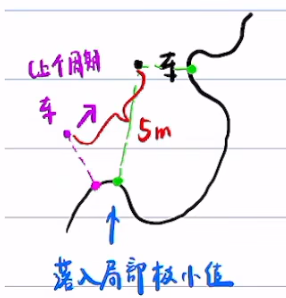
但是这种问题一般情况下不会出现,因为规划周期是100ms,即使以50m/s的速度运动,车也只走了5m,5m内道路不太可能出现这么扭曲的几何,一般在上个规划周期的匹配点上只有一个极值点。
万一真的出现这种情况:

使用 increase_count 变量记录\(l\)增加的次数
if \(l_{i+1}<l_i\) (\(l\)在减小)
increase_count = 0
if \(l_{i-1}<l_i\) 且 \(l_{i+1}>l_i\) (找到 \(l_{i}\) 为极小值)
存储 \(l_{i}\)
if \(l_{i+1}>l_i\) (\(l\)在减大)
increase_count++
if increase_count > 10 (意味着检查了10个点都没发现另外的极小值点)
break

第一次运行判断increase_count大于50个点,不是第一次运行则判断大于3个点
处理点不够的情况:
如果后面没有30m或者前面没有150m
解决办法:保持总长度不变(30+150),(10+170),(80+100)
轨迹拼接:

每100ms周期平滑的轨迹优大量重复的点,我们只需要将上一个规划周期和多出来的平滑轨迹拼接起来就可以
具体做法,将本周期和上个周期的参考线作比较,如果一模一样就用上个周期的平滑轨迹。若不一样,计算需要拼接多少个点记为n,
Fem Smoother 至少需要3个点才能够使用