算法与数据结构

认识复杂度、对数器、二分法

常数操作

基础运算（+、-、*、/）每一种运算所用的时间是相同的

例如1+1和54445486+522424242所用的时间应该是相同的，因为都是运行了int型的位数

寻址操作 所用的时间是差不多的

即使是数组，也只需要起始地址和偏移量即可

在单链表中的寻址操作所用的时间是不一样的（不是一个连续结构，所以不能使用偏移量）

常见的常数时间的操作：

• 常见的算数运算（+、-、*、/、%）
• 常见的位运算（>>、<<、>>>、|、&、^）
• 赋值、比较、自增、自减操作
• 数组寻址操作

复杂度

时间复杂度

时间复杂度：数据量为N的样本中，常数操作的次数的表达式的最高阶项。

\[ax^2+bx+c\]个常数操作的时间复杂度就是\(O(n^2)\)

需要把算法流程分解成常数操作\(O(1)\)

\(O\)指的是最差的数据情况下的时间复杂度

额外空间复杂度

除了样本空间和要求空间外，算法额外开辟的空间（自主空间）

常数项复杂度

• 放弃理论分析，生成随机数据直接测试
• 不是不能理论分析，而是没有必要，因为即使是固定常数时间，但是虽然都是常数操作但是，时间上也是不一样的，比如+法运算没有^运算快，/不如+快。

最优解

1. 时间复杂度尽可能低
2. 在时间复杂度尽可能低的情况下，空间复杂度尽可能低

常见时间复杂度排行

1. \(O(1)\)
2. \(O(logN)\)
3. \(O(N)\)
4. \(O(N*logN)\)
5. \(O(N^2)\)，\(O(N^3)\)，\(O(N^k)\)
6. \(O(2^N)\)，\(O(3^N)\)
7. \(O(k^N)\)
8. \(O(!N)\)

对数器

用时间复杂度高的差的办法来测试最优解的办法，差的办法和好的办法是都有可能出错的两套不同思路的算法，当两种算法的结果一样，即可验证。

当出现不一样的结果出现时，去锁定样本数据然后用手工的方法锁定被忽略的边界条件。

二分法

在有序数组中找到某个元素。样本数变化规律为 \[ N\rightarrow\frac{N}{2}\rightarrow\frac{N}{4}...1 \] 每一次找中间值为\(O(1)\)，一共有\(N\)个样本，每次取一半，时间复杂度为\(O(log_2N)\)。

:bulb:tips：

中点为\(mid=\dfrac{L+R}{2}\)

此时，\(L+R\) 可能会溢出，为了避免溢出，可以写成如下公式

\(mid=L+\dfrac{R-L}{2}\)

因为移位比除法更快，所以右移一位，写成代码为

mid = L + ((R + L) >> 1);

插入排序

冒泡排序

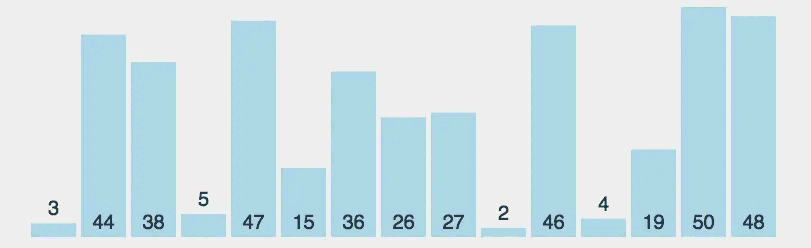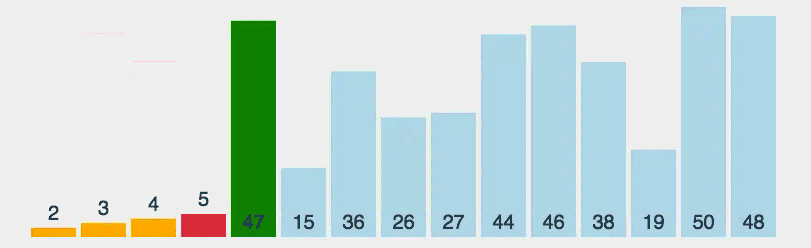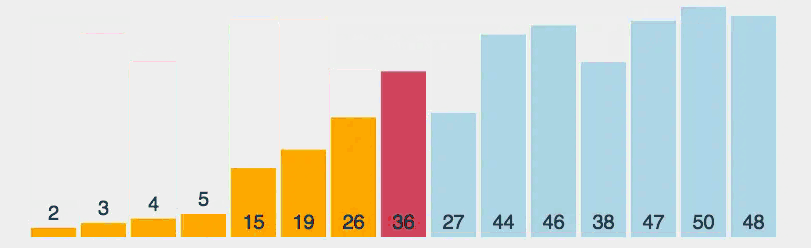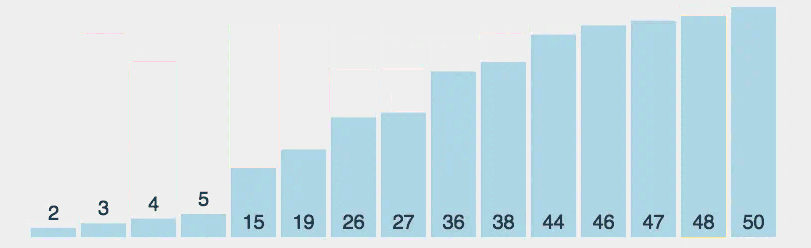
选择排序

思路：

1. 第一轮：找到最小的元素，跟数组第一个数交换
2. 第二轮：找到除去第一个数剩余元素的最小元素，跟数组的第二个数交换
3. 直到最后一个元素，排序完成

时间复杂度：O(n^2)

空间复杂度：O(1)

算法稳定性：不稳定

#include <iostream>
#include <vector>

using namespace std;

void selectionSort(vector<int> &nums) {
  for (int i = 0; i < nums.size(); ++i) {
    int min_index = i;
    for (int j = i + 1; j < nums.size(); ++j) {
      if (nums[j] < nums[min_index])
        min_index = j;
    }
    if (min_index != i)
      swap(nums[i], nums[min_index]);
  }
  for (int e : nums)
    cout << e << " ";
}

int main() {
  int N;
  cin >> N;
  int input_num;
  vector<int> nums;
  for (int i = 0; i < N; ++i) {
    cin >> input_num;
    nums.push_back(input_num);
  }
  selectionSort(nums);
  return 0;
}

选择排序