深度学习(二)
深度学习(二)
线性回归
线性模型可以看成是一个单层的神经网络
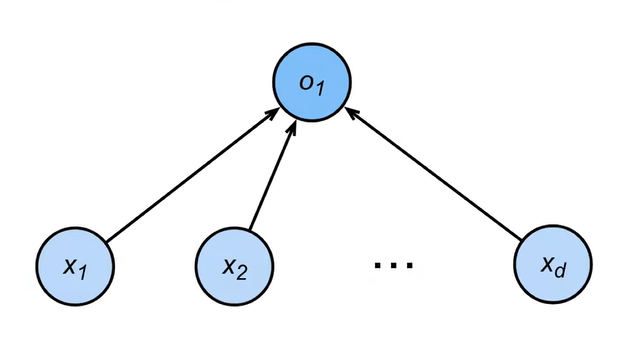
- 输入的维度是d
- 输出维度是1
- 每一个箭头都代表一个权重
衡量预估质量
假设\(y\)是真实值,\(\hat{y}\)是估计值,可以比较 \[ \ell(y,\hat{y})=\frac12\left(y-\hat{y}\right)^2 \] 叫做平方损失
里面的\(\frac{1}{2}\)是为了求导的的时候方便消去系数
训练数据
手机一些数据点来决定参数值,这些点被称为训练数据
通常越多越好
假设有n个样本,记: \[ \mathbf{X}=\begin{bmatrix}\mathbf{x}_1,\mathbf{x}_2,...,\mathbf{x}_n\end{bmatrix}^T\quad\mathbf{y}=\begin{bmatrix}y_1,y_2,...,y_n\end{bmatrix}^T \]
其中\(\mathbf{x}\)代表的是向量,y代表的是标量
参数学习
训练损失
\[ \ell(\mathbf{X},\mathbf{y},\mathbf{w},b)=\frac1{2n}\sum_{i=1}^n\left(y_i-\langle\mathbf{x}_i,\mathbf{w}\rangle-b\right)^2=\frac1{2n}\left\|\mathbf{y}-\mathbf{X}\mathbf{w}-b\right\|^2 \]
最小化损失来学习参数
\[ \mathbf{w}^*,\mathbf{b}^*=\arg\min_{\mathbf{w},b}\ell(\mathbf{X},\mathbf{y},\mathbf{w},b) \]
- 线性回归是对n维输入的加权,外加偏差
- 使用平方损失来衡量预测值和真实值的差异
- 线性回归有显示解
- 线性回归可以看作是单层神经网络
基础优化方法
梯度下降
挑选一个初始值\(w_0\)
重复迭代参数\(t=1,2,3...\) \[ \mathbf{w}_t=\mathbf{w}_{t-1}-\eta\frac{\partial t}{\partial\mathbf{w}_{t-1}} \]
沿梯度方向将增加损失函数值
学习率:步长的超参数
小批量随机梯度下降
在整个训练集上算梯度太贵
可以随机采样b个样本\(i_1,i_2,...,i_b\)来近似损失 \[ \frac1b\sum_{i\in I_b}\ell(\mathbf{x}_i,y_i,\mathbf{w}) \]
b是批量大小,另一个重要的超参数
线性回归实现
从回归到多类分类
回归:

- 单连续数值输出
- 自然区间R
- 跟真实值的区别作为损失
分类:
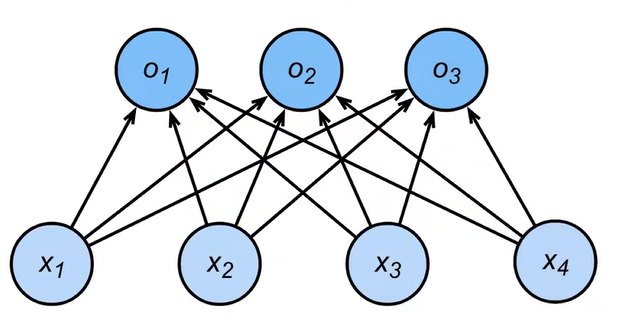
- 通常多个输出
- 输出i是预测为第i类的置信度
Softmax 回归
- 对类别进行一位有效编码
\[ \begin{aligned}&\mathbf{y}=[y_1,y_2,...,y_n]^\top\\&y_i=\begin{cases}1\text{ if }i=y\\0\text{ otherwise}&\end{cases}\end{aligned} \]
使用均方损失训练
最大值为预测\(\hat{y}=\arg\max o_i\)
需要更置信的识别正确类(大余量)\(o_y-o_i\geq\Delta(y,i)\)
输出匹配概率(非负,和为1) \[ \hat{\mathbf{y}}=\mathrm{softmax}(\mathbf{o})\\\hat{y}_i=\frac{\exp(o_i)}{\sum_k\exp(o_k)} \]
概率\(y\)和\(\hat{y}\)的区别作为损失
交叉熵常用来衡量两个概率的区别\(H(\mathbf{p},\mathbf{q})=\sum_i-p_i\log(q_i)\)
将他作为损失\(l(\mathbf{y},\mathbf{\hat{y}})=-\sum_iy_i\log\hat{y}_i=-\log\hat{y}_y\)
其梯度是真实概率和预测概率的区别\(\partial_{o_i}l(\mathbf{y},\mathbf{\hat{y}})=\mathrm{softmax}(\mathbf{0})_i-y_i\)
损失函数
L2 Loss 均方损失
\[ l(y,y')=\frac12(y-y')^2 \]
当预测值跟真实值离得越远,权重更新越大
L1 Loss 绝对值损失
\[ l(y,y^\prime)=|y-y^\prime| \]
权重更新幅度始终一直,不会根据预测值跟真实值差的多少变化,优点是稳定,缺点是在0点处剧烈震荡
Huber`s Robust Loss 鲁棒损失
\[ l(y,y')=\begin{cases}|y-y'|-\frac{1}{2}&\text{if}|y-y'|>1\\\frac{1}{2}(y-y')^2&\text{otherwise}\end{cases} \]
均方误差和绝对值误差结合