计算机图形学（一）

计算机图形学中的变换

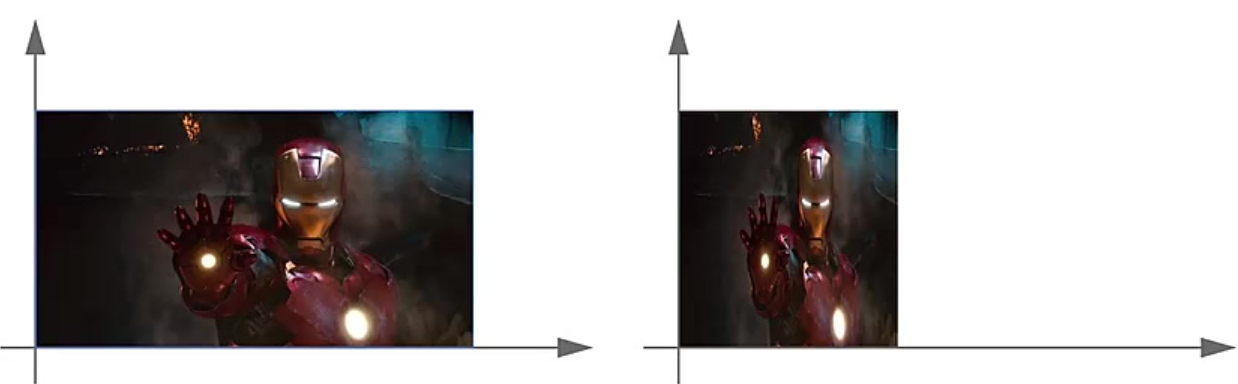
缩放 Scale

\[ M=\begin{bmatrix}S_x&0\\0&S_y\end{bmatrix} \]

\(S_x\)：x轴的缩放因子
\(S_y\)：y轴的缩放因子

\[ \begin{bmatrix}x'\\y'\end{bmatrix}=M\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}S_x&&0\\0&&S_y\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}S_x\cdot x\\S_y\cdot y\end{bmatrix} \]

当\(S_x\)或者\(S_y\)大于1的时候，图片沿着相应方向放大，当小于1的时候，沿着相应方向缩小。
当\(S_x=S_y\)的时候，图片按照比例放大缩小

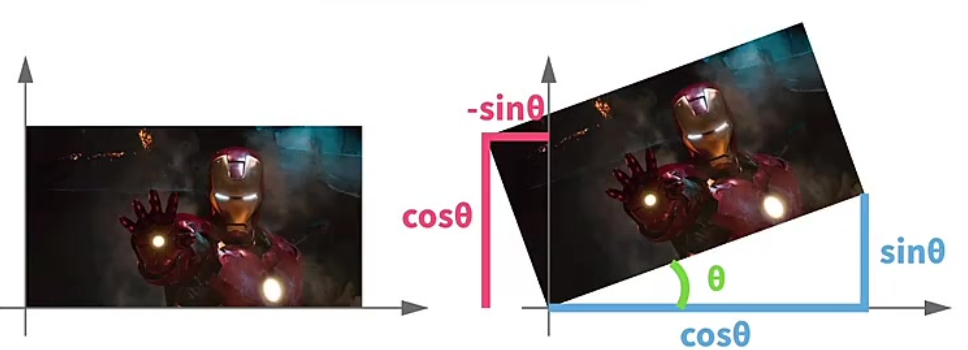
旋转 Rotate

\[ R(\theta)=\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{bmatrix} \]

\(\theta\)：逆时针旋转角度，单位是弧度

\[ \begin{bmatrix}x'\\y'\end{bmatrix}=R(\theta)\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}x\cos(\theta)-y\sin(\theta)\\x\sin(\theta)+y\cos(\theta)\end{bmatrix} \]

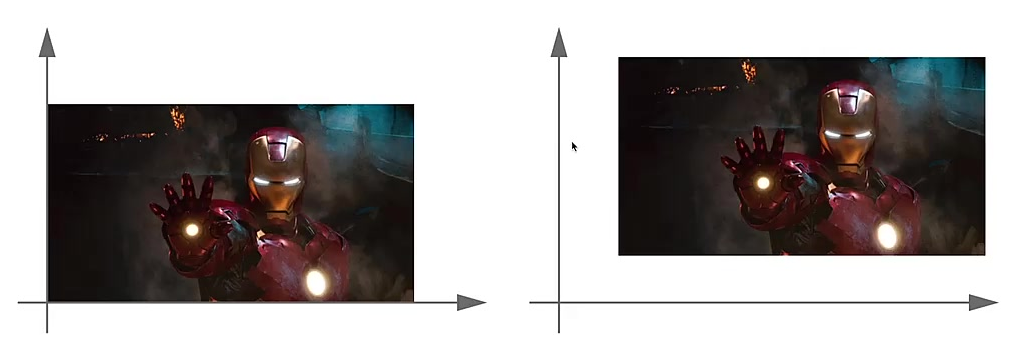
平移 Homogeneous Coordinatess

\[ 2\text{D point}=(x,y,1)^T\\2\text{D vector}=(x,y,0)^T \]

\[ T=\begin{bmatrix}1&0&T_x\\0&1&T_y\\0&0&1\end{bmatrix} \]

齐次坐标允许将平移、旋转、缩放等几何变换统一表示为矩阵乘法。这使得变换组合和计算更加简洁和高效。
一个二维点 (x,y)的齐次坐标表示为 (x,y,1)。这个表示方式允许通过矩阵变换进行各种几何操作，如平移、旋转和缩放。
一个二维向量 (x,y)的齐次坐标表示为 (x,y,0)。向量的最后一个分量是 0，这表示向量不受平移变换的影响，仅参与旋转和缩放等线性变换。

\[ \begin{bmatrix}x'\\y'\\1\end{bmatrix}=T\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}1&0&T_x\\0&1&T_y\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}x+T_x\\y+T_y\\1\end{bmatrix} \]